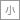北海道大学大学院工学研究院・工学院広報誌えんじにあRing　2011年10月号 ◆ハミルトニアンから材料まで　From Hamiltonian to skyscrapers

ハミルトニアンから材料まで
From Hamiltonian to skyscrapers

［PROFILE］
○研究分野／材料数理学、計算材料科学
○研究テーマ／合金の相安定性・相平衡・相変態の理論
○研究室ホームページ
　http://lms0-ms.eng.hokudai.ac.jp/japanese/homepage.html

Tetsuo Mohri ： Professor
Laboratory of Materials Modeling
Division of Materials Science and Engineering
○Research field : Computational Materials Science
○Research theme : Theory of phase stability, phase equliribria and phase 　transition of alloys
○Laboratory HP :
　http://lms0-ms.eng.hokudai.ac.jp/japanese/homepage.html

材料を分割すれば原子になる、しかし…
ミクロとマクロの中間領域に注目

　超高層ビルディングを支える鉄骨材料も、いろいろな電気製品に組み込まれた半導体材料も、私たちを取り巻く様々な材料を構成しているのが電子や原子であることは言うまでもありません。従って、新しい電気特性や強さを有する材料を設計するためには、電子の振る舞いや原子の結合の知識が必須です。しかし、私達が日常生活で目にしたり、用いたりしている諸々の材料の機能や特性は、原子や電子の振る舞いだけで決まるものではありません。電子や原子のスケールはオングストロームといわれる10^-8cm程度の領域にありますが、このようなミクロな領域と、日常で用いるcmやmといったマクロな材料のスケールには大きな隔たりがあり、ミクロな性質がそのままマクロな特性に反映されることはないのです。材料のマクロな特性を支配しているのはミクロとマクロの中間の領域（メソスケール）にある「内部組織」といわれるものです。内部組織は析出物、結晶粒界、転位等、結晶の中にある様々な欠陥の集合体によって構成されています。従って、マクロな材料を設計する為には、ミクロスケールにおける電子・原子の挙動を知った上で、メソスケールにおける組織の制御を行う必要があります。私達は、最近このようなマルチスケールにわたる材料設計をコンピュータを介して行う全国的なプロジェクトを開始しました（図1〜4）。

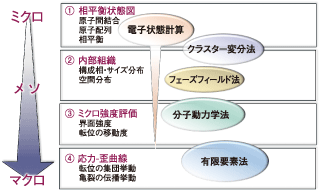図1 全国の計算材料科学者５名がミクロからマクロまでの手法を
　統合して材料のマルチスケール設計を行う。 Figure 1:Multi-scale computational materials designing by five experts over Japan

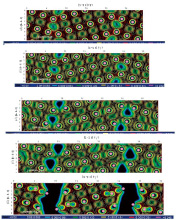図2 アルミニウムの結晶粒界の第一原理引っ張り試験。下図に向かって変形が増大し、界面から破壊が起こっている。（産業総合研究所、香山正憲氏提供）図2 アルミニウムの結晶粒界の第一原理引っ張り試験。
　下図に向かって変形が増大し、界面から破壊が起こっている。
　（産業総合研究所、香山正憲氏提供） Figure 2:First-principles tensile testing of Al grain boundaries (courtesy by Dr. M. Kohyama, AIST)

図3 Adaptive boost加速MD（分子動力学法）による転位運動や拡散挙動の加速解析。
　（大阪大学、尾方成信氏提供） Figure 3:Acceleration of dislocation movement and atomic diffusion by Adaptive boost MD
　(courtesy by Prof. S. Ogata, Osaka University)

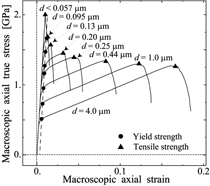図4 限要素法（弾塑性損傷構成モデル）に基づく応力—歪曲線の計算。
　結晶粒径への依存性を調べる。
　（物質・材料研究機構、渡邊育夢氏提供） Figure 4:Prediction of Stress-Strain behavior of poly-crystals with different grain size by Finite Element Method
　（courtesy by Dr. I. Watanabe, NIMS）

マルチスケール計算材料科学
「何故」の探求から「合成」へ

　量子力学のシュレディンガー方程式を解き電子・原子の振る舞いを把握して最適な原子の組み合わせを調べるのが最初の出発点です。「ハミルトニアンから」というタイトルはこのようなことを示唆しています。次に、フェーズフィールド法や分子動力学法といわれる強力な計算手法を用いて、原子の配列が乱れた転位や結晶粒界と言われる結晶の欠陥の振る舞いを調べ、計算機の中にこれらの集合体である内部組織を人工的に創り上げるのです。さらに、このようにして創った内部組織が集まったときに示すマクロな特性を、有限要素法という手法をもって計算機の中で測定します。このように、従来の計算材料科学は「何故か」を解析することに力点が置かれていたのに対し、このプロジェクトでは、計算機の中に新たな材料を「合成する」ことにも力を傾注します。そして、これまでの材料は一様なものが良いとされてきましたが、計算機の中にいろいろなヘテロな内部組織を創り出すことで、新しい特性をもつ材料を設計することを目指しています。