特集 01
量子力学がより身近になる21世紀に Quantum mechanics is getting closer to YOU in the 21st century

「量子力学? と思うあなたに」
応用物理学部門 数理物理工学研究室
助教
小布施 秀明
Chapter 01
夢物語だった量子コンピューターが現実に
みなさんは「量子力学」あるいは「量子○○○」という言葉を聞いたことがありますか?最近では日本をはじめ世界各国の名だたる企業が「量子コンピューター」(図1)の開発を競っています。なかでもアメリカのIBMにある量子コンピューターはネット上から誰でも無料で利用できるため、今後北大の講義でも活用される場面が出てくるかもしれません。私が学生の頃は“夢物語”だと思われていた量子コンピューターが、こうして実用化に向けて一歩ずつ進んでいることを思うと、現代のテクノロジーの進化に感嘆するばかりです。

2017Macmillan Publishers Limited, part of Springer Nature
Chapter 02
猫の生死が「重なり合う」不可思議な量子力学
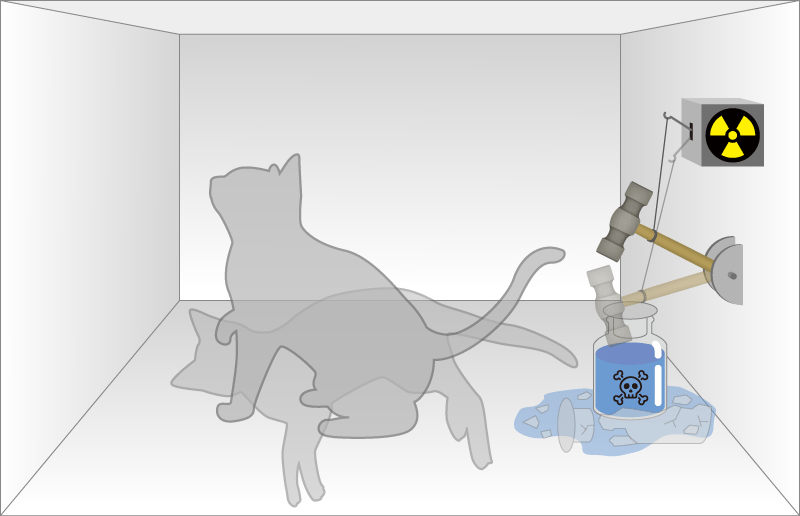
量子力学の本質的かつ不可思議な性質を象徴する用語に「シュレーディンガーの猫」(図2)という思考実験があります。よく小説などでも引用されることがあるようです。毒ガスが50%の確率で発生する密閉した箱の中に猫を閉じ込めると、箱を開けない、すなわち観測しない限り、箱の中で猫が生きている状態と死んでいる状態が“重なり合って”同時に存在することを意味します。この“重なり合う”という状態は、量子力学ならではの表現です。私たちの日常で「シュレーディンガーの猫」のような現象に遭遇することはまずありませんが、量子力学は現実世界の不可思議な自然現象を記述するのに極めて重要な理論であり、20世紀前半に確立した学問です。
Chapter 03
金属の鉄と絶縁体のダイヤ電気伝導特性の違いを明らかに
では、量子力学がなければ説明できない自然現象とは何でしょう?例えば、物質を極低温まで冷やすと電気抵抗がゼロになる超伝導現象もその一つであり、さらに身近な例をあげると金属と絶縁体もその一例です。鉄は鉄原子、ダイヤモンドは炭素原子が規則正しく周期的に並んだ結晶ですが、前者は電気をよく流す金属で、ダイヤモンドは電気を流さない絶縁体。全く異なる電気伝導特性を示します。この電気伝導特性の違いも電子の運動を量子力学によって記述することで初めて説明できるようになります。量子力学は意外と身近な存在なのです。
Chapter 04
「二重スリットの干渉実験」波のようにもふるまう粒子
「量子」の存在が明らかになったのは20世紀初頭の頃。光(電磁波)のエネルギーが連続的に変化するのではなく、実はとびとびの不連続な値を示すことがわかり、エネルギーの最小単位量が粒のようなもの、「量子」であることが発見されました。量子の一種類に光の粒子、光子(こうし:フォトン)があり、有名な「二重スリットの干渉実験」(図3)によって光子は波の性質も持つことが明らかになっています。すなわち光子は、粒子と波の両方の性質を備えており、これを「粒子と波動の二重性」といいます。この性質は光子に限らず、量子力学に従う粒子が等しく持つ性質です。電子も二重スリットを通過すると[図4(a)]、スクリーンに到達した1つの電子の場所を表す白い点の現れ方にムラが生じ、干渉効果を起こすことが確かめられています[図4(b)]。
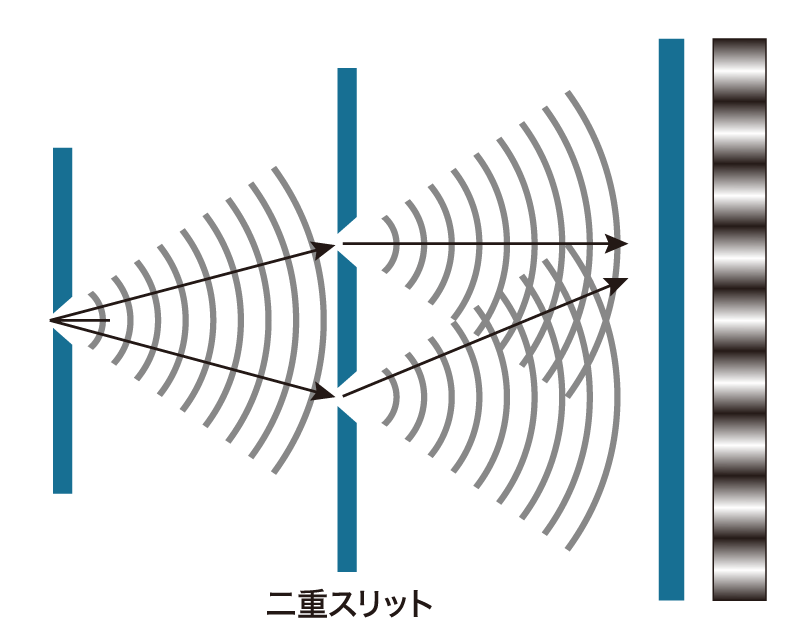
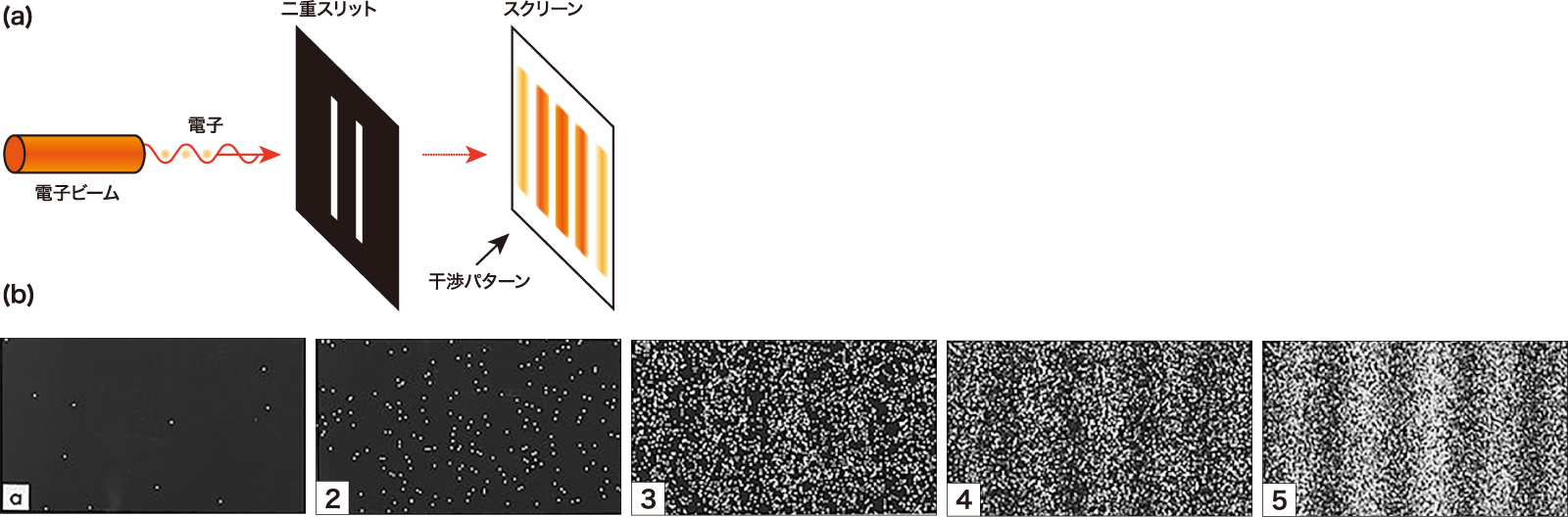
A. Tonomura, J. Endo, T. Matsuda, and T. Kawasaki,“Demonstration of single‐electron buildup of an interference pattern”, American Journal of Physics 57, 117 (1989)
Chapter 05
量子力学の運動方程式はシュレーディンガー方程式
ここで、思考実験「シュレーディンガーの猫」を提唱したオーストリアの物理学者エルヴィン・シュレーディンガーが提案した、量子力学に従う粒子の運動方程式である「シュレーディンガー方程式」を見てみましょう。
質量mの粒子が直線のx軸上を自由に運動する場合は、次のように記述されます。ψはギリシャ文字で「プサイ」と発音します。
ψ(x,t)を波動関数、ℏを換算プランク定数といい、iは虚数単位を表します。左辺はψ(x,t)の時間tについての微分、右辺は位置xについての微分であり、シュレーディンガー方程式は偏微分方程式なのです。
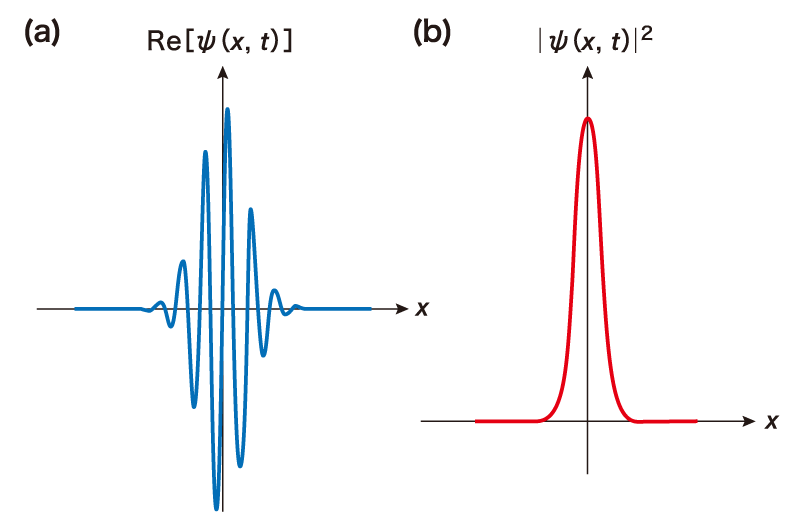
ψ(x,t)は粒子の量子力学的状態[図5(a)]を表し、波動関数という名から分かる通り、シュレーディンガー方程式では粒子の状態を波として記述します。さらに量子力学では、|ψ(x,t)|2が、時刻t、位置xにおける粒子の存在確率に比例すると解釈します[図5(b)]。古典力学とは異なり、たとえ初期状態が正確に分かっていても確率的にしか粒子の運動を予測することができません。また、波動関数ψ(x,t)は通常複数の状態の“重ね合わせ”となっており、これを説明する思考実験が「シュレーディンガーの猫」なのです。
私がこの式を初めて見たとき、「これで世界の根本理論が説明できるんだ!」と衝撃を受け、この式を理解したくて物理の道に進みました。わからないからこそ惹かれてしまう。これは、量子力学に限らず、全ての学問に共通するものだと思います。
Chapter 06
新物質が続々と発見「トポロジカル絶縁体」
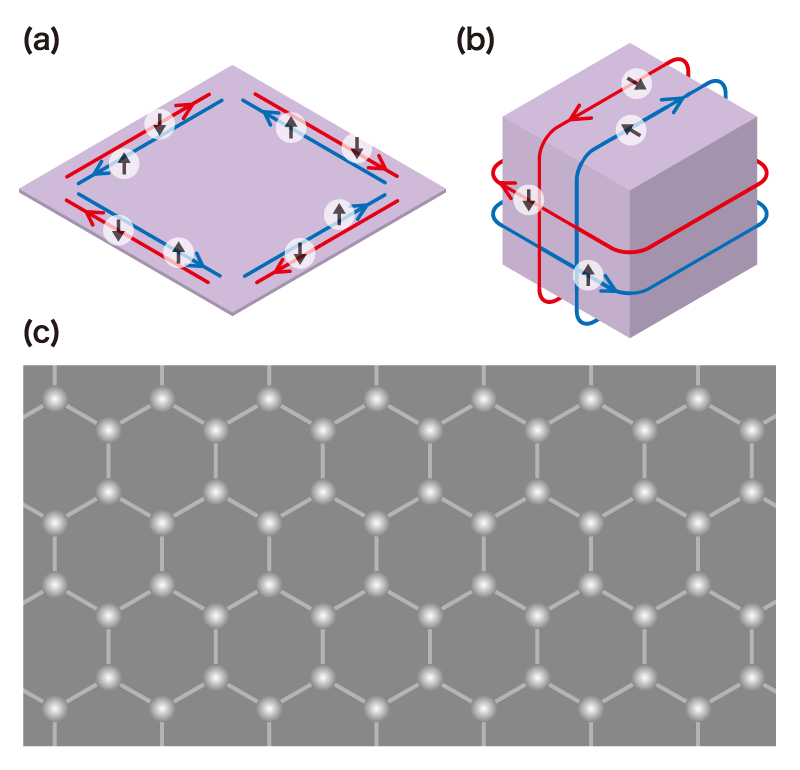
現在も量子力学の研究は日進月歩で進んでおり、新物質が続々と発見されています。例えば15年ほど前に発見された「トポロジカル絶縁体」[図6(a)、(b)]は金属とも絶縁体とも異なる特異な電気伝導特性を持ち、世界中の物理学者により精力的に研究が行われています。トポロジカル絶縁体中の電子の運動が、前述したシュレーディンガー方程式ではなく、相対論的量子力学の「ディラック方程式」で説明されるところも我々研究者にとって新たな驚きでした。
また同時期に発見された、炭素原子が平面上のハニカム構造になっている「グラフェン」[図6(c)]も、その中の電子の運動がディラック方程式に従うため、非常に特異な電気伝導特性を示します。グラフェンはすでに応用段階にあり、近い将来みなさんの身の回りにグラフェンを用いた電子機器が登場するかもしれません。
Chapter 07
21世紀の量子力学をみなさんの手で!
一口に量子力学といっても複数の専門分野に枝分かれしており、まだ理論的にも未整備な領域が随所に残っています。冒頭に触れた量子コンピューターの発展と並行して、我々研究者が互いの領域を行き来することでさらに新たな発見や理論が生まれる可能性に満ちています。興味がある人はぜひ、北海道大学で量子力学の扉をノックしてみてください。より詳しい入門書として長岡洋介先生が書かれた『基礎物理学シリーズ・現代物理学』(東京教学社)もお勧めです。