|
レーザー冷却 Laser cooling レーザー冷却とは 通常光が当たると物体は暖かくなります。日なたにいると暖かいですよね。ではどうしてレーザーで冷却ができるのでしょうか? 光が物体(固体)に吸収される時、まず物体中の電子が光子のエネルギーを吸収して加速されます。 その運動は瞬時に多数の原子へと伝わっていき、熱的な運動に変換されます。 そのため、光子のエネルギー(\(\hbar\omega\))はそのまま熱エネルギーに変換され、物体が加熱されます。
\(\Delta E_{solid} = \hbar\omega\)
ところが、気体中の原子では状況が大きく異なります。 気体中の原子は孤立しています。そのため原子が光を吸収して電子が加速された後、他の原子にエネルギーを分け与えることなく、自然放出で光子を放出して元の状態に戻ってしまいます。 そのため、光子はほとんど原子にエネルギーを与えません。 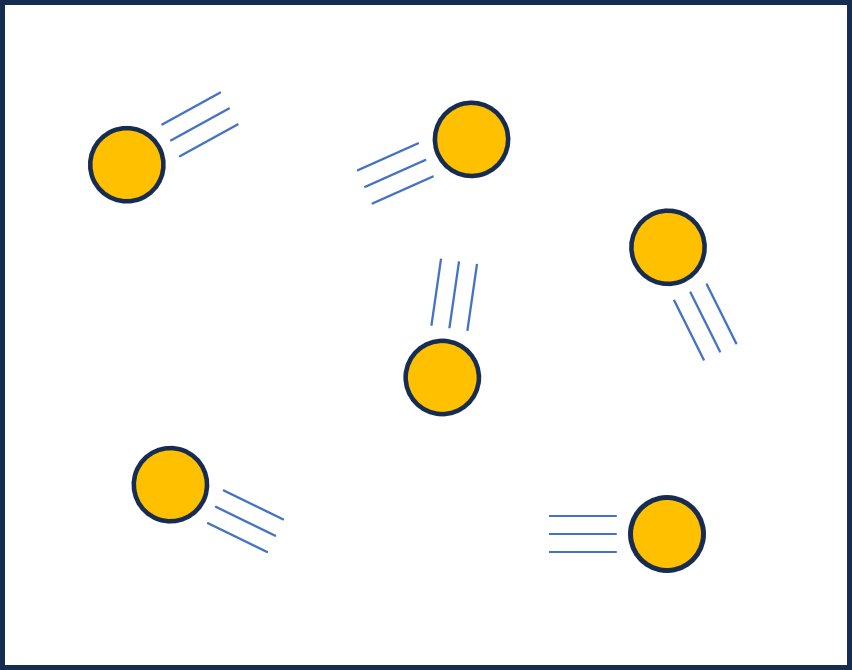 ここで光子の運動量(\(\hbar\vec{k}\))を考えましょう。 原子は吸収した光子と放出した光子の差分の運動量を受け取っています。 自然放出はすべての方向にランダムに起きますので、平均すると吸収した光子の運動量分だけ原子は押されることになります。 そのため、原子の運動と光の進行方向が同じ向きのときは原子は加速(加熱)されますが、それらが互いに逆向きであれば原子は減速(冷却)されます。 ただし、そのエネルギー変化は光子のエネルギーよりも6桁ほども小さいものです。
\(\Delta E_{atom} = \frac{|{m\vec{v}+\hbar\vec{k}}|^2}{2m}-\frac{|{m\vec{v}}|^2}{2m}\sim \hbar(\vec{k}\cdot \vec{v})\ll\hbar \omega\)
レーザー冷却は、このような光子の持つ小さな運動量を用いて原子を冷却します。 1回のエネルギー変化は小さいのですが、これを10000回ほど繰り返すことで、原子は常温の\(\sim300K\)から絶対零度付近の\(\sim100\mu K\)まで冷却されます。 その時間はわずか\(1ms\)程度です。 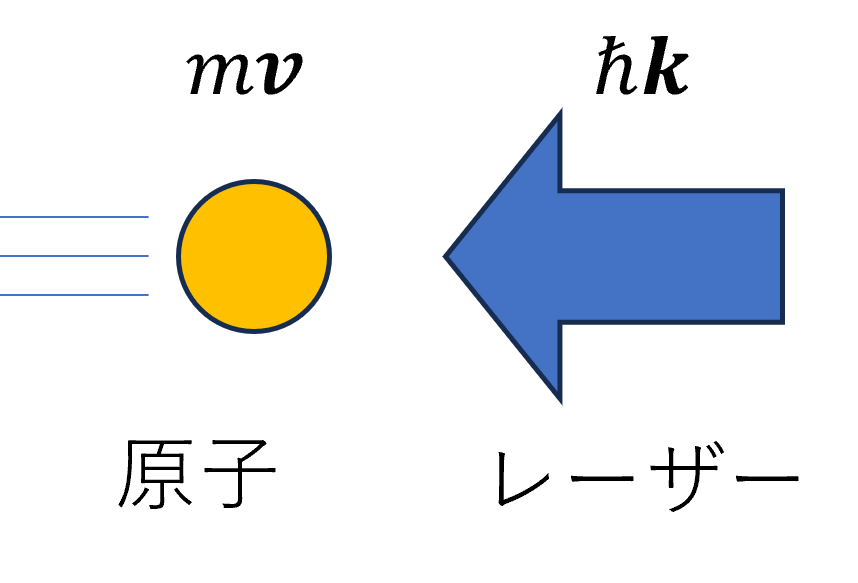 ドップラー冷却 原子の熱運動はランダムなので、単にある方向からレーザーを当てても冷却にはなりません。ではどうすれば冷却になるのでしょうか? そのためには、原子の構造とドップラー効果の理解が必要です。  原子は、重い原子核と軽い電子から構成されています。 電子の原子核の周りでの運動を量子力学を使って解くと、電子はいくつかの特定のエネルギー状態にだけ存在できることが分かります。 ここでは単純化して、エネルギーが最も低い状態(基底状態)と次に高い状態(励起状態)の2つの状態だけを考えます。 通常電子は基底状態にありますが、励起状態と基底状態のエネルギー差と同じエネルギーを持つ光子が飛んでくると、その光子を吸収して励起状態に遷移します。 このように、特定の周波数の光のみが吸収されまして、その周波数は共鳴周波数と呼ばれます。 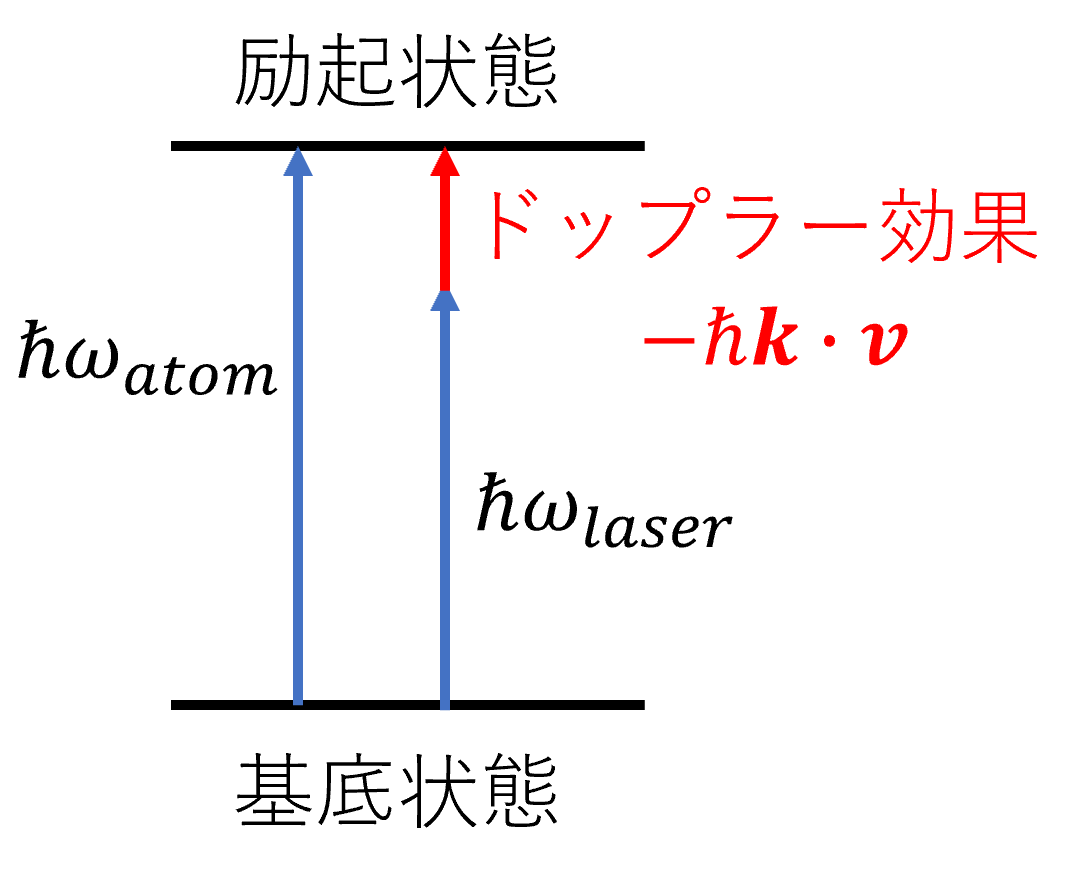 ここで、レーザーの周波数を共鳴周波数よりも少し低くしておきます。 そうすると、レーザー光と逆向きに進んでいる原子は、ドップラー効果によってレーザー周波数を高く感じるので、レーザー光を吸収し減速されます。 レーザー光と同じ方向に進む原子はドップラー効果で周波数をより低く感じるので、吸収は起きず加速はされません。 すなわち、冷却だけが起きます。  実験では、このような周波数のレーザーを直交する6方向から入射します。 そうすると、原子はどの方向に進んでもその方向と逆向きのレーザー光を吸収し減速されるので、3次元的な冷却が実現されます。 このような、ドップラー効果を利用したレーザー冷却はドップラー冷却と呼ばれており、代表的なレーザー冷却法となっています。 冷却限界温度とさらなる冷却 では原子はどこまでも冷えるのでしょうか? 原子はレーザー光を吸収するときだけではなく、自然放出するときも運動量を受け取ります。 この方向はランダムなため平均すると0になりますが、運動量の揺らぎ(分散)を与えます。 この運動量の分散は自然放出の回数に比例して増加していき、加熱となります。 このランダムな自然放出による加熱とドップラー冷却による冷却が釣り合うときの温度がドップラー限界温度と呼ばれ、\(100 \mu K\)ほどになります。
\(T_\rm{Doppler} = \frac{\hbar\Gamma}{2k_B}\sim 100 \mu K\)
ドップラー冷却以外のレーザー冷却法も考案されており、偏光勾配冷却やRaman冷却と呼ばれる手法があります。 これらはドップラー冷却によって冷却された原子をさらに冷却するために使われており、これらの冷却限界温度は反跳温度と呼ばれる\(100 nK\)程度です。
\(T_{recoil} = \frac{(\hbar k)^2}{2mk_B}\sim 100 nK\)
ただし、このようなレーザー冷却だけでは原子の密度を上げることが困難です。 そこで、レーザー冷却された原子を、磁場や光を使って空間的に閉じ込めておき、その中で蒸発冷却と呼ばれる高エネルギー原子を選択的に逃がす方法によって、高密度かつ極低温に冷やす実験が行われています。 この蒸発冷却を進めると、ボース-アインシュタイン凝縮やフェルミ縮退と呼ばれる量子統計性の強く現れた非古典的な気体が生成されます。 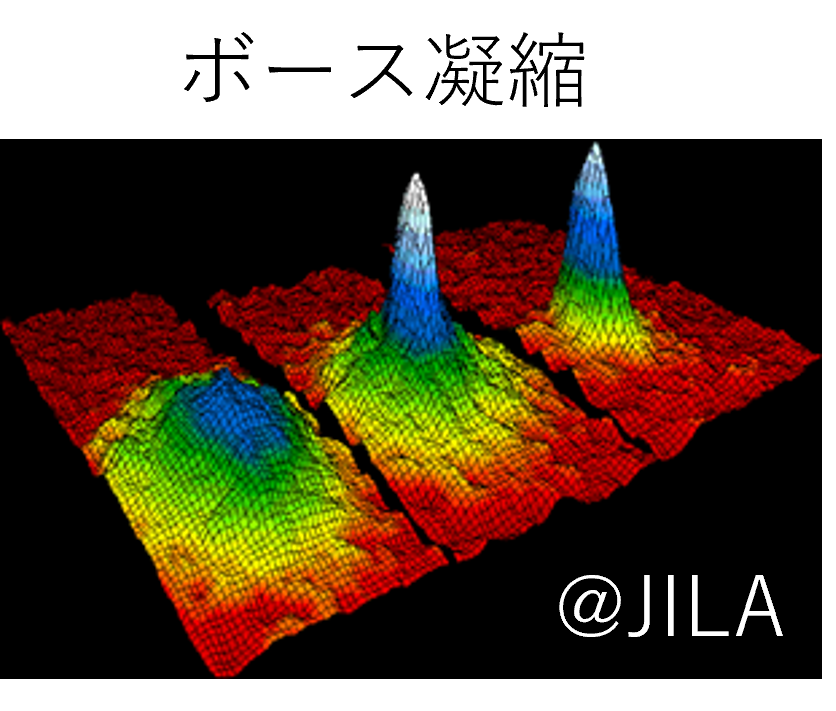 そのような気体は、超流動性や超伝導性を持つ他の物理系と類似の性質を持つことから、冷却された原子を使って、他の物理系を再現する量子シミュレーションと呼ばれる研究が盛んです。 さらに、冷却原子を用いた量子コンピューター開発も急速に進められており、ますます注目の集まる研究分野となっています。 戻る © 2024 Laboratory of Photonics Engineering, Hokkaido University. All rights reserved. |