拡散係数を求める方法
拡散の実験は解析が難しいらしく、
時々文献から大きく外れた値を報告する人を見掛けます。
解説記事(旧版)も用意したのですが、
パソコンを使いこなすのが困難な人は、それでも解析に手間取るようです。
そこで手作業だけでも解析ができるよう、
解説記事を書き直してみました。
前半部分(1〜8まで)は少々退屈な濃度への換算の説明なので、
軽く読み流しても良いでしょう。
-
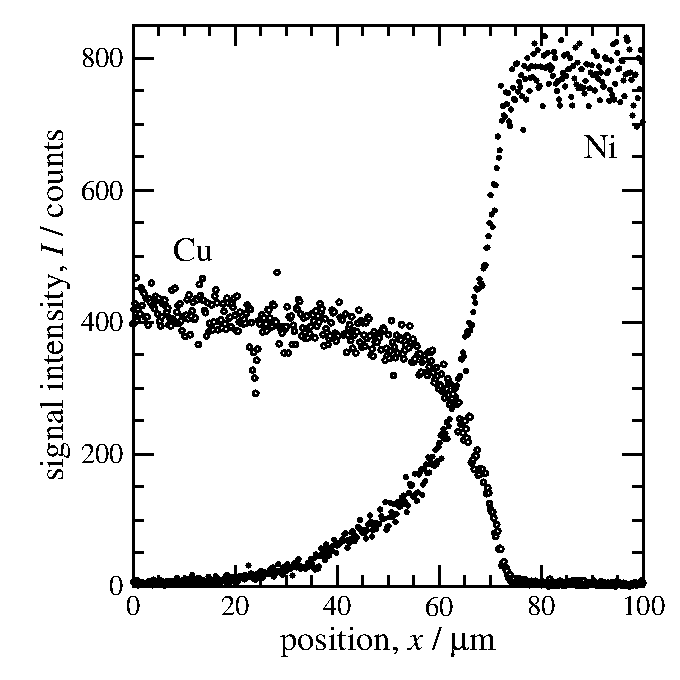
まずはEPMAの測定結果をグラフにする(図1)。
縦軸は機械から出て来たままの特性X線の計数である。
銅もニッケルも濃度は滑かにある値から0へと変化しており、
相互拡散が起きていることを示している。
なおこのグラフは (このページの冒頭で述べた事に反して)
手作業だけで作るのは困難であるけれど、
同等なものを用意して学生実験の時間などに配布するから大丈夫。
|
図1 EPMAの測定結果。○が銅、●がニッケルの結果である。
元の画像はきちんと区別がついたのだが、JPEGに変換する際に
シンボルが潰れてしまって区別がつかない。
|
-
EPMAの計数のままでは解析できないので、
実験データを組成に変換する必要がある。
EPMAの計数は濃度に比例していると考えて換算すればよい。
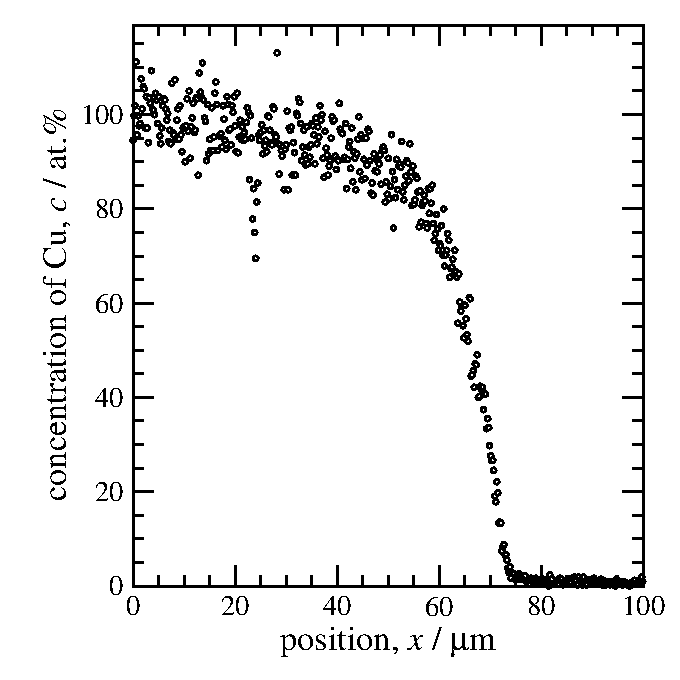
たとえば図1で銅の計数は x = 0 µm の地点では
I = 400 を少し越えている位なので、
銅の計数を4.2で割ってみると、
お手軽に濃度プロファイルが得られる。
|
図2 図1に掲げたEPMAの測定結果を4.2で割り算したグラフ。
図1から銅のプロファイルだけ取り出してある。
縦軸の範囲は100から減るようになり、濃度っぽい。
|
-
ただし、EPMAの計数は統計的なバラつきを持っているので
注意しなければならない。
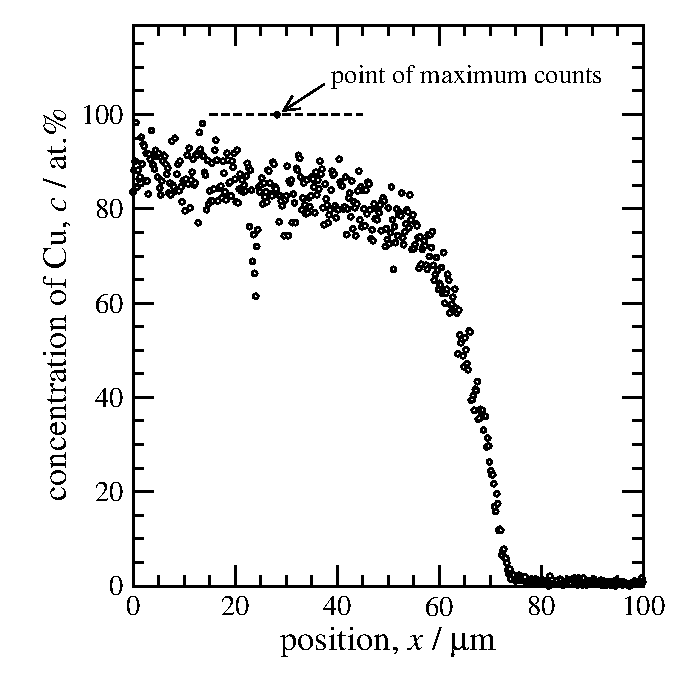
Cuの計数の最大値はx = 28.25µmにおける
I = 475なのだが、
この475が100%になるように変換すべく
計数を4.75で割ると、
グラフの左端が90%位にしかならず、
濃度を表す曲線としては不合理である。
機械的に最大の計数を調べて換算の係数を決めてはいけない。
|
|
図3 変換係数を誤った結果。
|
-
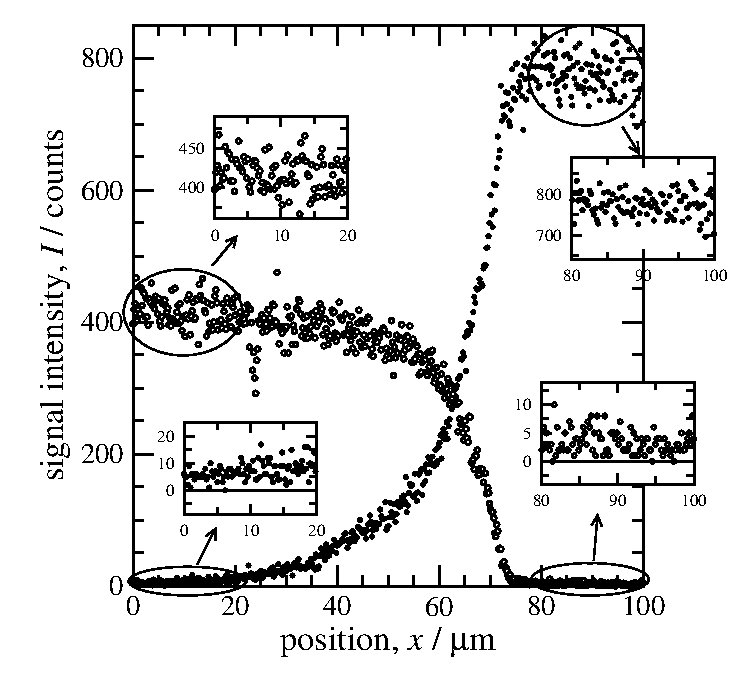
図1のグラフの四隅を拡大したものを図2に示す。
バックグラウンドの計数はI = 3 位
("さんい"ではなく、"さんぐらい"と読んで欲しい)、
純ニッケルの計数がI = 780 位、
純銅の計数はI = 420 位であろう。
拡大図を見るとニッケルの銅側への拡散プロファイルは
x = 0 においても傾きを持っており、
最後まで測定し切れていないことがわかる。
計数の分布を調べれば、Poisson分布をしていることがわかり、
バックグラウンドの平均値などもきちんと求められるはずなのだが、
Higgs粒子を探しているわけでもないので、
目分量で解析すれば十分である(学生実験だし...)。
そして目分量であれば、
バックグラウンドの3は無視してしまっても差し支えない。
実際、銅が100%近い組成を持つx < 20µmの領域に着目すると、
データは400から450回という50カウントの範囲を越えてバラツイており、
この計数の誤差を濃度に換算するならば、
ここでの測定誤差は10%を越えている。
この値は濃度プロファイル中で最大の
相対誤差であるが、
1%未満の小さな誤差は問題にならないのは理解できると思う。
|
図4 EPMAの測定結果。バックグラウンドと計数/組成の
変換係数を求めるために純銅、純ニッケルの領域を拡大して
表示してある。
|
-
上の結果から
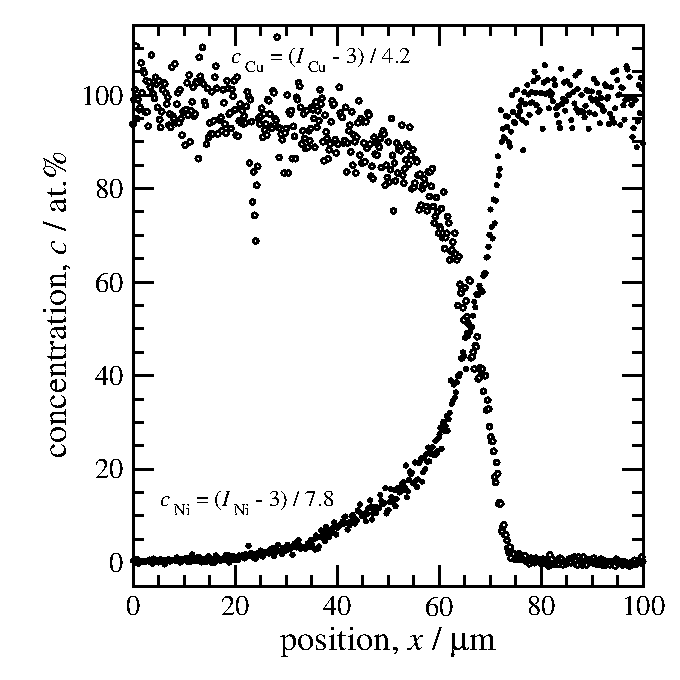
銅の計数は3を引いて4.2で割り、ニッケルの計数は3を引いて7.8で割る。
これで「100%満点」に換算できる。
全てのデータ点の測定結果を4.2で割ったりするのは、
とても手間のかかる仕事で手作業では無理と思えるかも知れないが、
実際にしたことは、
縦軸の数値のラベルを書き直すだけである。
ニッケル濃度に対しては780と書いてある所を100とするだけのことである。
|
図5 バックグラウンドを補正して、純銅・純ニッケルを
濃度100%に
換算した濃度プロファイル。
|
-
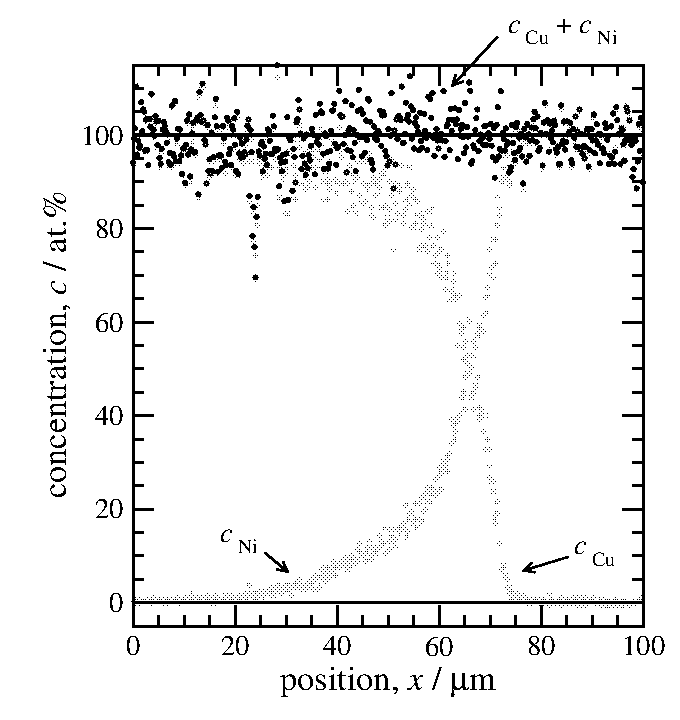
参考のために銅の濃度とニッケルの濃度を足し合せると
100%になることを確認(図6)してみる。
±5%の誤差はありそうに見える。
|
図6 各点における組成の和。
濃度100%の線からのズレが濃度の
測定精度を示している。
|
-
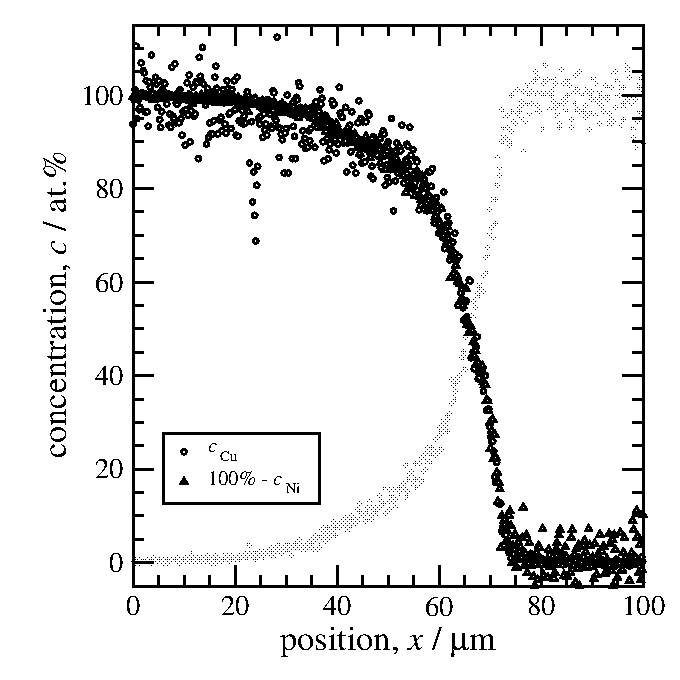
図6とは異なる視点からのアプローチ。100%からニッケルの濃度を引くと
銅の濃度と等しいはずである。確認してみた(図7)。
当然二つのプロファイルは良く一致している。
|
図7 銅の濃度プロファイル。銅からのシグナル強度を直接
換算したデータと、
100%からニッケル濃度を引いたデータを比較。
|
-
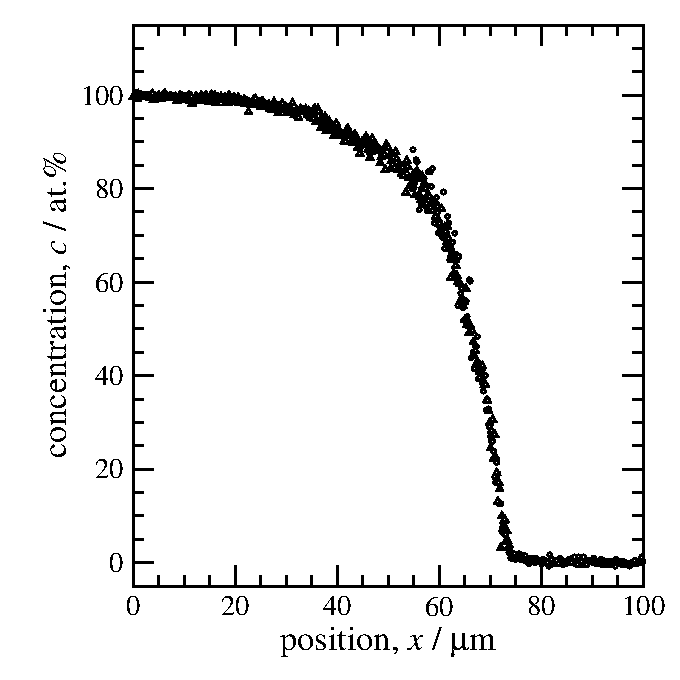
ちょっと寄り道して、バラツキが大きいデータをトリミングしてみた(図8)。
EPMAは信号強度が強い程、計数のバラツキの絶対値は大きくなる。
銅0%ではバラツキは±3程度なのに、100%では±30以上の
バラツキを持つ。バラツキの小さいデータ同士を繋げてシェープアップ。
|
|
図8 図7のバラツキが小さいデータをつないだプロファイル。
|
-
すこり寄り道が過ぎた。
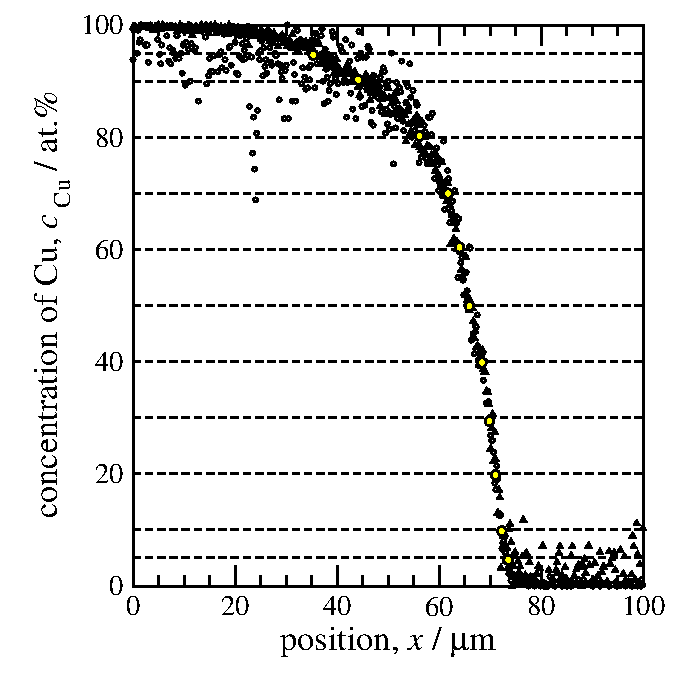
上に述べた手順2.で
得られたプロファイル曲線から、銅の濃度が
5%、10%、20%、30%... 80%、90%、95%に
なる点の座標を拾い上げる(図9)。
|
図9: 銅の濃度プロファイルから10%刻みに
点を拾った様子を示す図。
選んだ点は黄色の丸で示されている(良く見えないが...)。
|
-
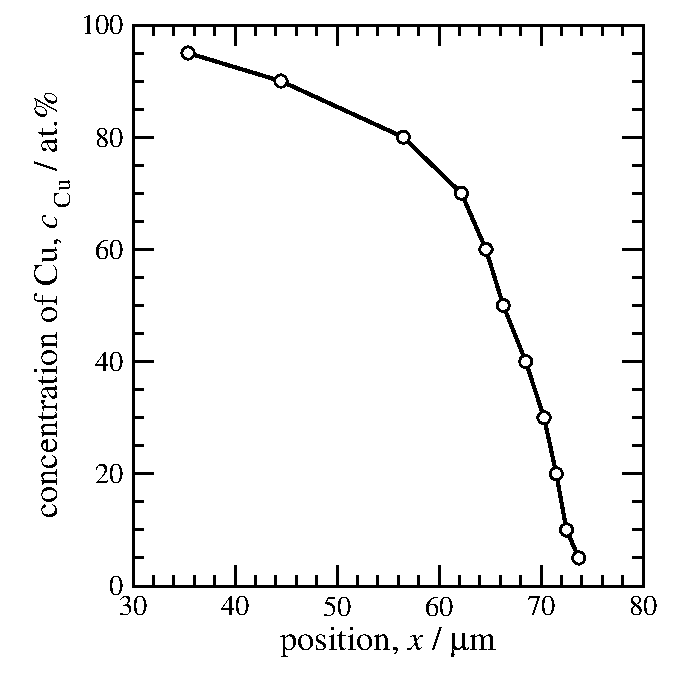
図9で拾い上げた点を抜き出してみた。
|
|
図10: 実験の濃度プロファイルから10%刻みで取り出した点。
|
-
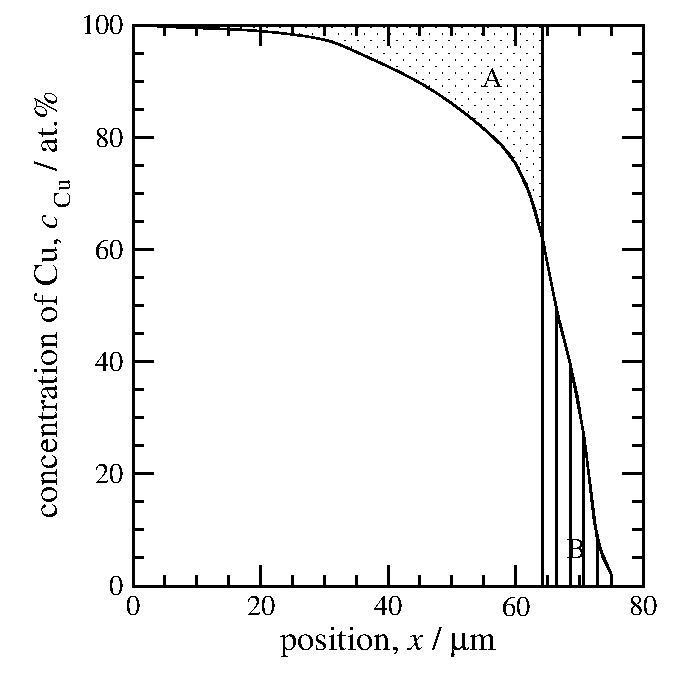
次に俣野界面を求める。
下に挙げた濃度プロファイルを示す図11で、
Aと書いてある影をつけた部分と、
縦縞で示したBと書いてある部分の面積が等しくなるように
境界線を決めなさいということである。
|
図11: 俣野界面の説明図。上図の影を付けた部分(A)の面積と
縦縞の部分(B)の面積が等しくなるように線を引く。この図の
例ではBの方が少し小さそうなので、真の俣野界面はもう少し
左側に寄った所にあるのだろう。
|
-
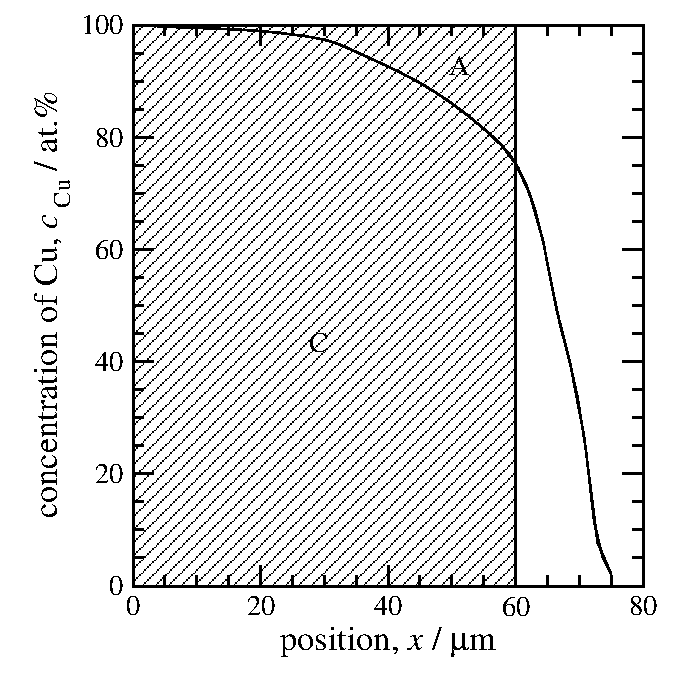
何度も線を引き直して、図11のAとBが等しくなるまで
試行錯誤を繰返すのでは大変であろう。
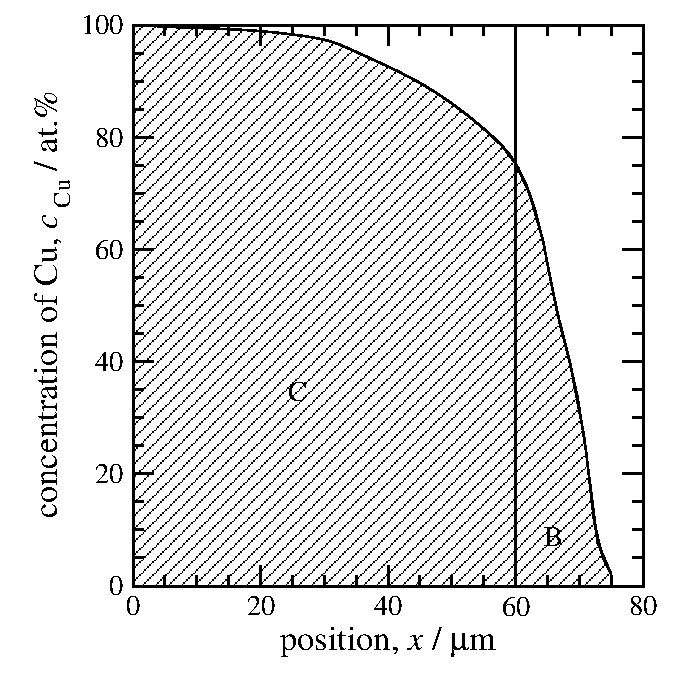
実は簡単に俣野界面の位置を決める方法がある。
図12の左側の斜線を施した領域の面積をまず求め、
それと等しい面積を持つ長方形を描いてみる(図12右図)。
(図12左の斜線部分) = (図12右の斜線部分) ならば
B + C = A + C ということだから、
(Bの面積) = (Aの面積)となり、これは正に俣野界面を決める条件である。
|
|
|
図12: (賢い)俣野界面の求め方。
|
-
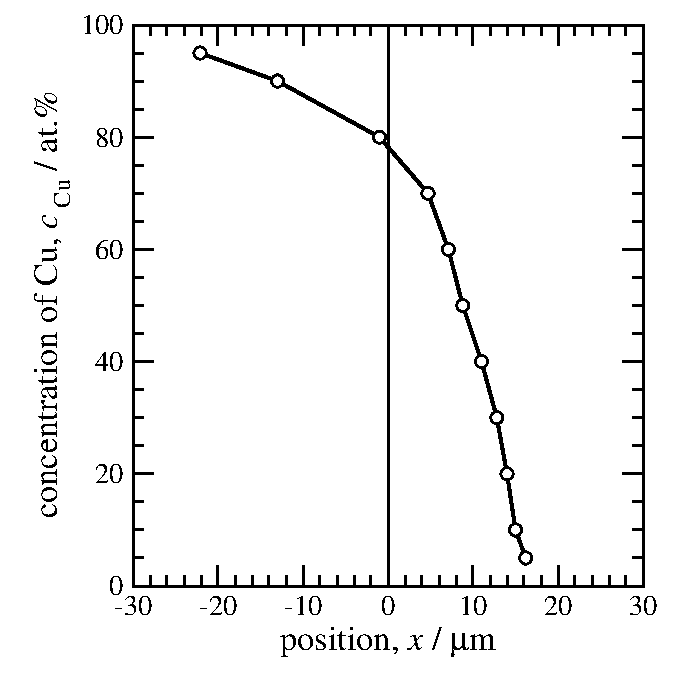
俣野界面の座標が分ったら、座標原点を俣野界面に移す。
この操作も横軸のラベルを貼り替えるだけである。
|
|
図13: 原点を俣野界面に移した濃度プロファイル曲線。
|
-
異なる時間、熱処理を施した試料についても同様の処理をする。
すなわち、10%刻みにデータの位置座標を読み取り、
俣野界面を決める。
-
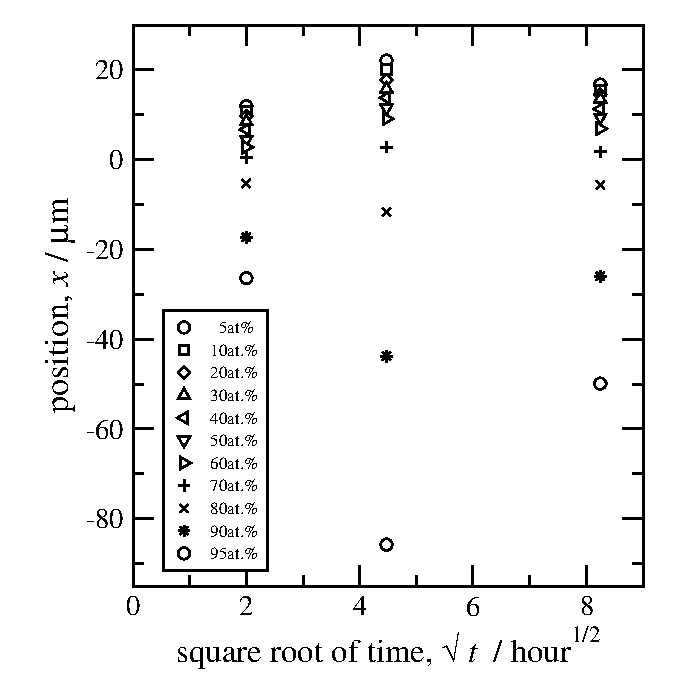
横軸に熱処理時間の平方根、
縦軸に10%刻みに拾い上げた座標を取ってグラフを作る。
縦軸の座標は俣野界面を原点とする座標である。
図9で10%刻みで読み取った点の座標値から
俣野界面の座標を引けば良い。
|
図14: 異なる熱処理時間の試料の拡散距離の比較。
68時間熱処理した試料の拡散距離は、20時間熱処理のものより
拡散距離が小さいように見える。
|
-
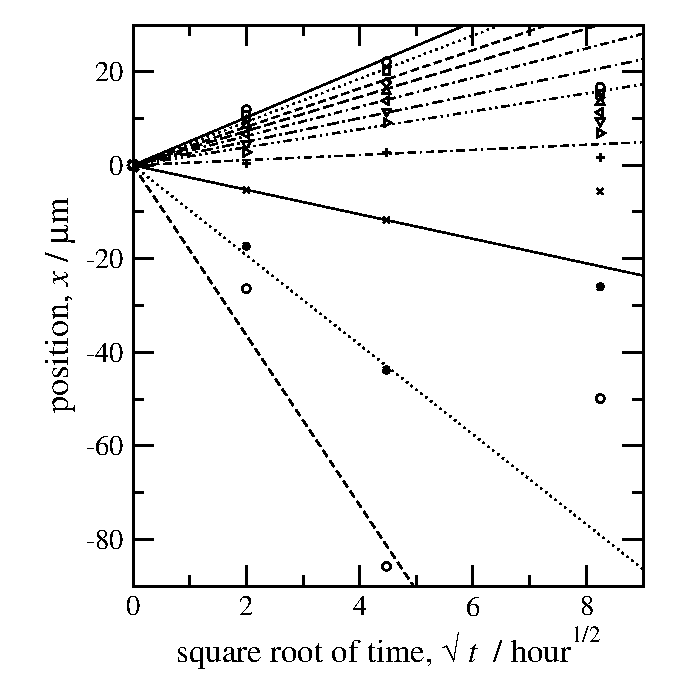
俣野解析は濃度プロファイルが x/(t)1/2 の関数で
書くことができるということを前提としている。
つまり図14で描いたグラフは原点を通る(半)直線になるはずである。
データを検討して線を引く。
下に示す図15では、熱処理時間がt=64時間
(t1/2=8時間1/2)のデータ点が
直線にのるようには線を引きずらい。
64時間熱処理した試料のデータは軽く見て(というか、殆ど無視して)
線を引いてある。
95%を示す点は具合が悪いが、他はそこそこ良く線を引くことができる。
|
図15: 拡散距離の熱処理時間依存。
原点を通るように直線を引こうとしても無理があるようだ。
|
-
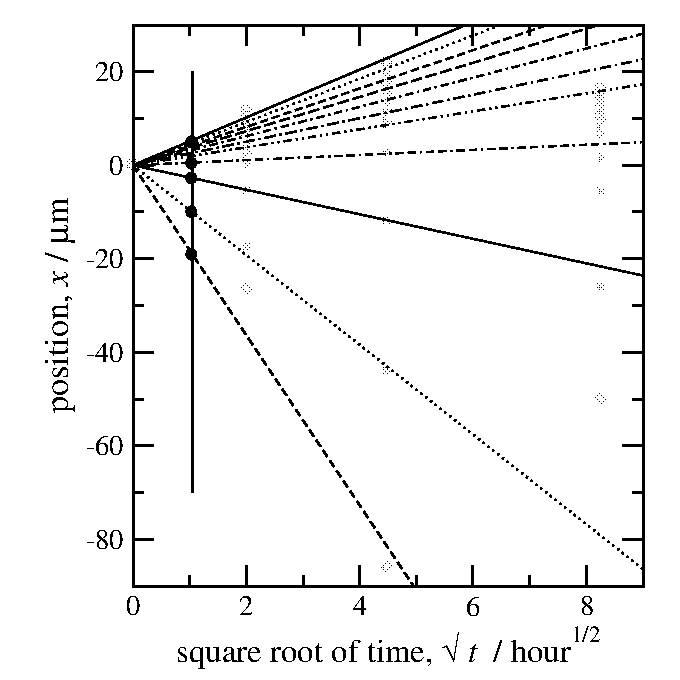
t = 1時間の所で線を引いてみて、
1時間後の濃度プロファイルの形状を推定する。
図16に例を示す。
3個の試料のデータの重みを付けた平均になっているので、
1回だけの実験結果よりも信頼性の高いデータが得られる。
また、図15で測定点が直線に乗っているかどうかを調べることで、
俣野解析の妥当性を評価することにもなっている。
半直線同士の間隔が狭くてデータを読み取りづらいなら、
36時間後でも100時間後でも好きな時間を取って良い。
|
図16: 1時間後の濃度プロファイルの推定。
半直線とt1/2=1の交点の位置座標を読み取る。
|
-
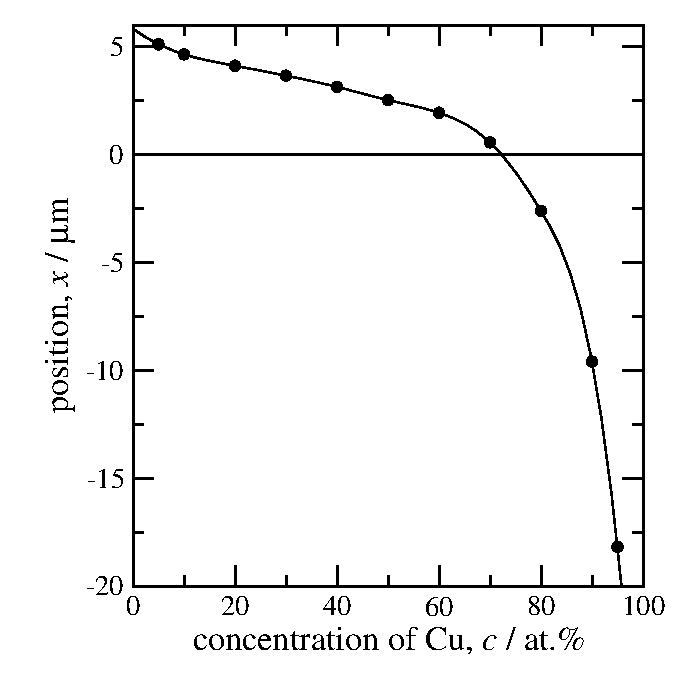
横軸を濃度、縦軸を座標に取って、1時間後の濃度プロファイルを描いてみる。
|
|
図17: 予想される1時間後の濃度プロファイル。
|
- あとはテキストの付録の手順に従って、
各組成での拡散係数を求めれば良い。
-
拡散係数は拡散距離を濃度の関数と見た時のグラフの
微係数と定積分が分れば計算することができる。
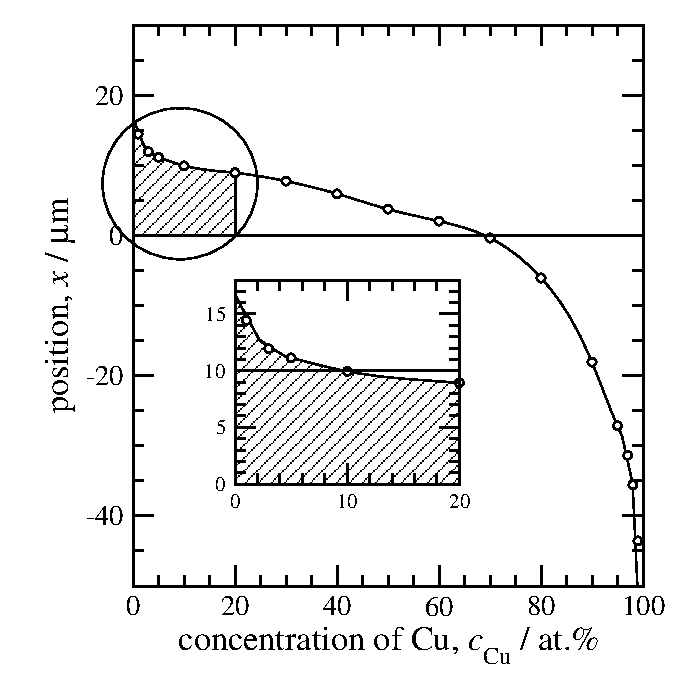
図18に例として20at.%における拡散係数の求め方を示す。
定積分は図18の左の図で斜線を施した部分の面積で与えられる。
210µm·at.%位であろうか。
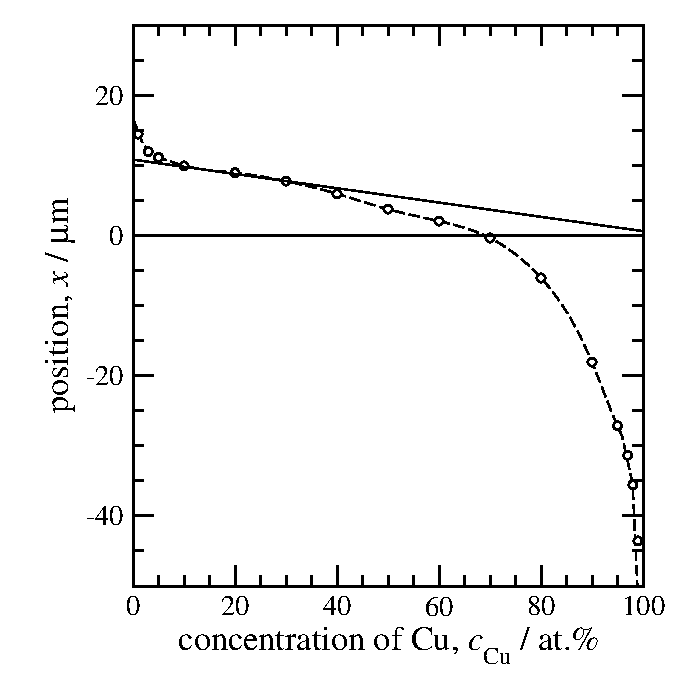
微係数は図18の右側の図に示した接線の傾きで与えられる。
微分を正確に求めるのは難しいのだが、100%濃度が増加すると
距離は10µm程減少しているので、
傾きは-0.1µm/at.%位になるだろう。
|
|
|
図18: c = 20at.%における拡散係数の計算。左の図が積分、
右の図が微分を求める所である。
|
拡散係数を求める式
| |
1 |
∂x |
∫ |
c |
|
|
D(c) = -
|
----- |
----- |
|
x dc |
| |
2t |
∂c |
0 |
|
にこれらの値を代入して、拡散係数は
D = (1/7200)× 0.1 × 210
= 2.9×10-3 µm2/s
と求まる。



















