Snowflakes are letters from heaven.
In 1936 Prof. Ukichiro Nakaya had succeeded to make artificial snow at Hokkaido university. He showed that small difference at the growing condition produces various structures of snow crystals. After him, anomalous shapes of crystals have been created in crystallography. At last, we discovered the topological crystals. They are classified by the concept of topology. Topology is one of the subjects in mathematics that argued size-independent universality of mathematical structures. This concept is necessary to understand the unconventional topologically-nontrivial forms of the crystals. We investigate universality of mathematical structures in crystallography at the viewpoint of topology.

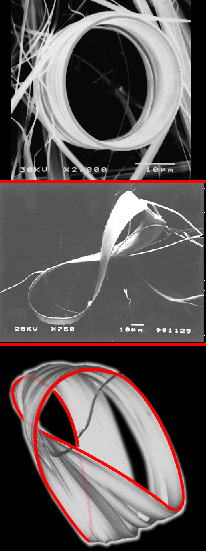Crystals are usually the materials in which the atoms align periodically. However, the topological crystals are locally corresponding to the usual crystals locally but globally not because the ends of the crystals are connected. The crystals are rings. Moreover, the twisted rings such as the Moebius rings with p twist and figure-of-eight loops with 2p twist have been discovered. These forms can be categorized using topology, and the crystals cannot be changed its topological form without cutting of chemical bonding. The topological property of crystals has been neglected in crystallography for the bulk crystals. Our discovery has opened new era of crystallography at the viewpoint of topology. Figure 1. Topological crystals Ring, figure-of-eight, and Moebius ring of crystals Satoshi Tanda, Taku Tsuneta, Yoshitoshi Okajima, Katsuhiko Inagaki, Kazuhiko Yamaya, and Noriyuki Hatakenaka　Nature 417, (2002) 397

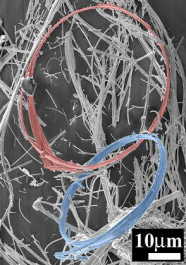Exotic topological crystals, such as ring-shaped crystals, Moebius strips of crystals, and figure-of-eight (2p-twisted strip) crystals, have been successfully created in NbSe3, despite their inherent crystal rigidity. Recently, we discovered new topological crystals in TaSe3, which are two ring-shaped crystals linked to each other exactly at once. Due to the link the two rings cannot be separated without cutting of chemical bonding. The topology of the crystal form is called a "Hopf link", which is the simplest link involving just two component unknots linked together exactly once. The Hopf link topology must be categorized using the concept of manifold-embedding. These crystals have been expected to open new fields of quantum mechanics on the nontrivial topological space and crystallography on topological boundary conditions. Figure 2. Realized Hopf link topology in crystallography J. Cryst. Growth 297 (2006) 157, T. Matsuura, M. Yamanaka, N. Hatakenaka, T. Matsuyama, and S. Tanda

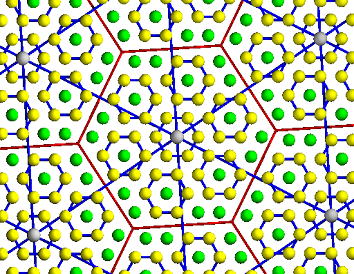Some crystals have anisotropic growth and conductivity due to the crystal structures. Transition metal trichalcogenide is the typical one. One transition metal atom and three chalcogen atoms are accumulated and growth one dimensionality. The conductivity is also one-dimensional. Therefore, such low-dimensional materials exhibit peculiar ground states not shown in three dimensional systems. Density waves (CDW and SDW), integer and fractional quantum Hall states, Tomonaga-Luttinger liquid state are good example of ground state of the low dimensional electron systems. Usual dimensionality control methods can be categorized three types. Using naturally low dimensional materials, Using micro-fabrication technique to make lower dimensional systems, Pressuring materials to make overlapping of electron's wave function to change them higher dimensional systems. We fabricate naturally low dimensional materials to make strong low dimensional systems and investigate new phenomena using them. Figure 3 shows hierarchical charge density wave structure in two-dimensional electron system. We discovered number of electrons in nth clusters follows the progression law An+1＝9An−2. This law realizing the hierarchical honeycomb structure is a universal structure that is derived mathematically when cluster growth in two-dimensional triangle lattice system is in the condition of the hierarchical nature and maximum packing. We investigate universal structure in low dimensional materials using the dimensionality control method. Figure 3. Hierarchical charge density wave structures caused by k-space topology in nano crystals Seven atoms make a cluster, then seven clusters make a super cluster. T. Toshima. K. Inagaki. N. Hatakenaka. S. Tanda. J.Phys Soc. Japan 75 (2006) p024706