|
基礎量子物理学の研究のための物質波を用いた量子光学実験 A Neutron Optical Approach to Explore the Foundation of Quantum Mechanics はじめに 量子力学の予測が正しいことは様々な系を用いた実験で高精度に確証されてきた。 量子力学は相対性理論と並んで「現代」物理学で大きな役割を果たしており、 その適用範囲は物理学のみならず、化学や生物学の領域にもわたっている。 さらに、この理論は物性物理学の発展に大いに寄与し、現代の科学技術の開発基盤になっている。 このような「成功」の裏で、量子系で何が起こっているのかといった、 量子力学の解釈に関しては統一的な見解があるとは言えない。 総じて、量子力学を理解しようとすればするほど、実在、因果律、 局所性などの我々の慣れ親しんでいる世界から離れることを余儀なくされる。 すなわち、量子力学はいまだにミステリーに満ちあふれている。 中性子光学実験 物質波による量子力学的効果の観測には、ヤングの二重スリットのように二つの光線が合わさった時にみられる干渉縞を観測するのが一般的である。 このような、干渉効果の観測のための機器は干渉計と呼ばれ、中性子の物質波による干渉計は70年代に開発された(図1参照)[1]。 こうした中性子干渉計を用いて、1/2スピンの4π周期性、中性子の質量を利用した重力ポテンシャルの影響、 トポロジカルな量子力学的位相(あるいはベリー位相、幾何学的位相とも呼ばれている)等を観測する実験などが行われてきた。 また、スピンの重ね合わせの実験などはまさに最近のキュービットの実験の先駆けともいえる。 あるいは、確率論的ではなく決定論的な予測を量子力学に与えるべき理論の一つとしての隠れた変数理論に関する実験も行われている[2]。 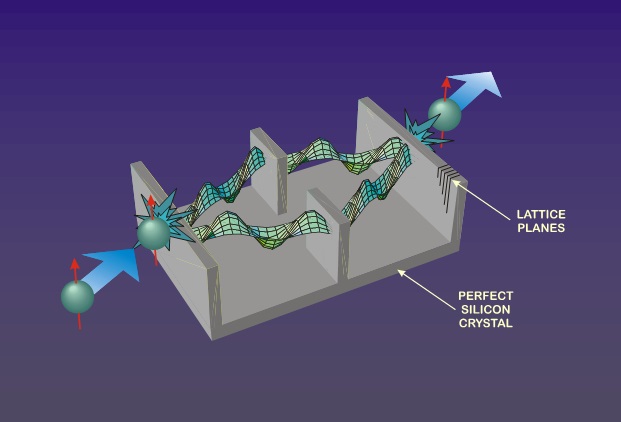 図1:中性子用の干渉計のイメージ図。 上記のような干渉計を用いた光学実験以外にも、中性子のスピンの干渉を利用した中性子偏向解析装置(ポラリメータ)を使っても量子光学実験が可能である。 干渉計実験では2つの経路の状態が基底状態になっているのに対し、この偏向解析装置ではアップとダウンの2つのスピン固有状態が基底状態になる。 スピンの重ね合わせ実験で示されたように、スピンの基底状態の相対位相は出射ビームの偏向解析をすることにより測定できる。 この中性子偏向解析装置を用いて、中性子でのアハラノフ・ボーム(AB)効果の検証や、量子力学の基本である非可換なオブザーバブルに関する実験が行われた[2]。 量子チェシャ猫の実証実験 [3] ナノの世界で起こる現象は量子力学によって記述され、不確定性原理をはじめ、 波動と粒子の二重性、状態の重ね合わせのなど、日常の経験からすると奇異な現象が多く存在する。 テルアビブ大学のアハラノフ教授らが理論的に導出した新現象は、児童小説『不思議の国のアリス』に出てくる「チャシャ猫」にちなんで、 「量子チェシャ猫」と名付けられた。 通常の推察では「中性子とスピンは粒子とその粒子の性質」なので、分離不可分であるが、 今回の研究では、この粒子とスピンの空間的な分離を中性子を使った光学実験で実証した(図1参照) 。 実験では、中性子干渉計に入射した中性子が2つの光路の分れた後、それぞれの光路で適正なスピン操作にあう。 この2つの光路は干渉計を出射する際に再び合わせられ、「事後選択(post-selection)」と呼ばれるスピンの選択が行われ検出器に入る。 この段階で「量子チェシャ猫」が出現する。 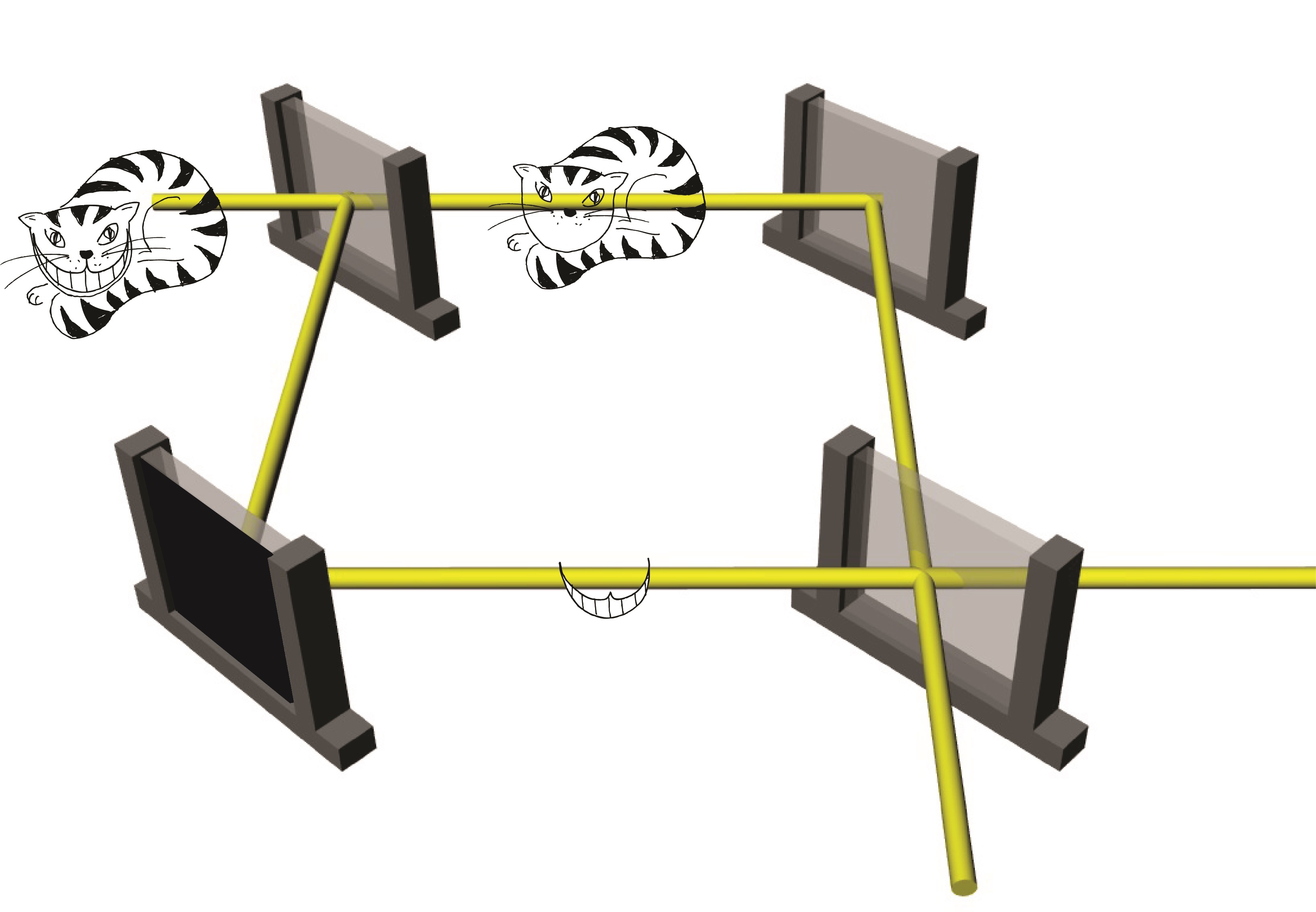 図2:量子チェシャ猫のコンセプト。 さまざまな不確定性関係とその検証実験 ハイゼンベルクが提唱した不確定原理[4]を実験的に扱った初めての研究を行った。 不確定性原理はいわゆる量子力学の草創期に示された確率解釈、粒子と波動の2重性、 相補性等とともに新しい量子力学の特異性を示す事象の一つである。 この原理によると、量子力学に従う「粒子」のすべての性質を同時に任意の正確さで決定することは不可能であり、 ハイゼンベルク自身によって示されたガンマ線顕微鏡の例のように、以下のように根拠づけられてきた。 すなわち、或る一つの測定はいつでも必然的に測定対象の「粒子」に変化をもたらし、これによって別の性質の測定にを誤差を生じさせる、という。 しかし、その定量的定式化は事態はそれほど単純ではなく、正確な不確定性関係の記述には測定の誤差や擾乱といった物理量を定義することから始める必要があった。 厳密な測定理論の取り扱いをへて、小澤は2003年に一般化した不確定性関係を導出した[5]。 不確定性関係の検証実験のコンセプトを図2に示す。 この実験では、基本的に、ある状態に準備された量子系にたいしてAとBのインコンパチブルな連続測定を想定している。 このとき、前段の測定はオブザーバブルAで表わされる測定であるべきだが、実際に測定で使用されたのはオブザーバブルOAで表される測定である。 このズレが直接的に測定の誤差に寄与する。 実際の実験では、中性子の1/2スピンのxとy成分の測定、 すなわち非可換なパウリ行列 σx と σy で表わされる測定における測定誤差と擾乱に関する不確定性の関係を調べた。 今回の実験の目的は、実験結果がハイゼンベルクの不確定性関係(3)か小澤の不確定関係(4)どちらの関係を示すかをみることである。 得られた結果によると、小澤の不確定関係は常に下限よりも大きいことがわかった。 次に、ハイゼンベルクの積は、今回の実験の範囲では、常に下限よりも小さいことが分かった。 つまりこの実験で、ハイゼンベルクの不確定性関係が成立せず、小澤の不確定関係が成立することが検証された[6]。 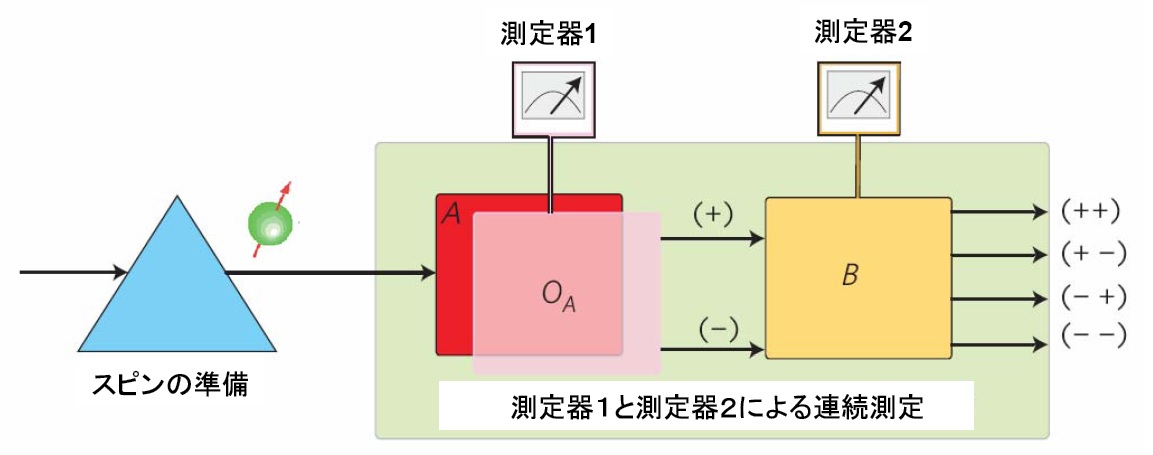 図3:不確定性関係の実験的検証のコンセプト。 参考文献 [1] H. Rauch, S.A. Werner, Neutron Interferometry, Clarendon Press, Oxford (2000). [2] J. Klepp, S. Sponar, and Y. Hasegawa, Prog. Theor. Exp. Phys. (2014) 082A01. [3] T.Denkmayr, H. Geppert, S. Sponar, H. Lemmel, A. Matzkin, J. Tollaksen, and Y. Hasegawa, quant-ph/1312.3775, Nature Comm. 5:4492 doi: 10.1038 / ncomms5492 (2014). [4] W. Heisenberg, Z. Phys. 43 (1927) 172. [5] M. Ozawa, Phys. Rev. A 67 (2003) 042105. [6] J. Erhart, S. Sponar, G. Sulyok, M. Ozawa, G. Badurek, and Y. Hasegawa, Nature Physics 8 (2012) 185-189. リンク http://www.neutroninterferometry.com/ 戻る © 2018 Laboratory of Photonics Engineering, Hokkaido University. All rights reserved. |