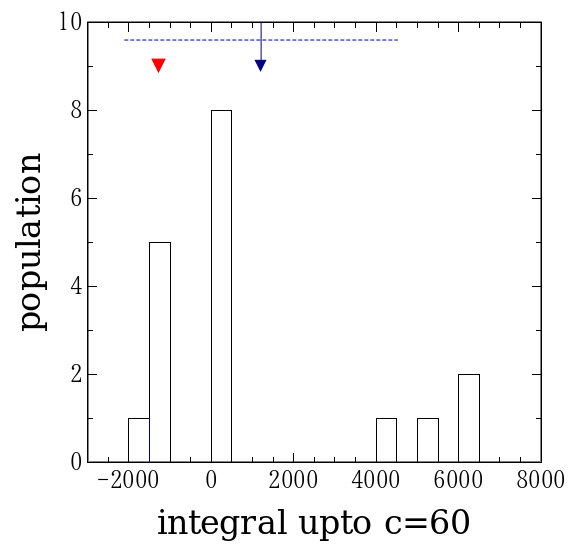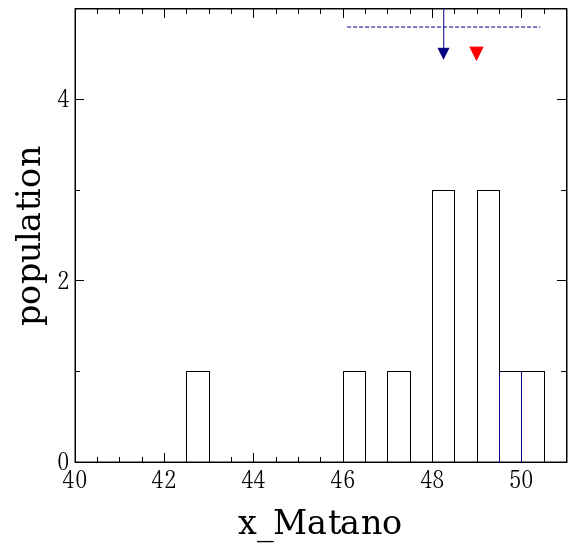
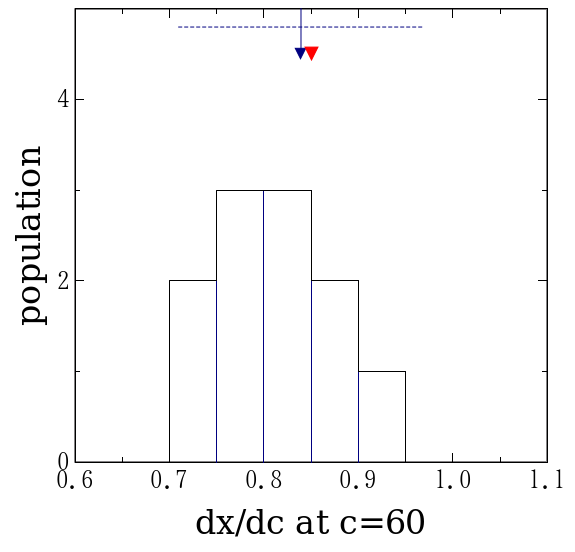
俣野演習IIの結果報告

材料工学実験を履修している人達の協力を得て、 グラフを読み取る時の誤差がどの位あるかを調べる実験を行なった。 小論ではその結果を報告する。

まず、報告された俣野界面の位置(図1)、60%における接線の傾き(図2)、 0%から60%までの積分(図3)の分布を示す。 報告された値の平均値が紺色の矢印、厳密値が赤の三角形で示してある。 また、平均値±標準偏差の範囲を紺色の破線で示した。 平均値と誤差の範囲の表示の仕方は以下同様である。 報告された値の平均 ± 標準偏差の範囲に 厳密解が含まれていることが分る。 それだけを見れば結構なことに思えるが、積分の分布を見ると I = -1270位であるべきところを、標準偏差は3000を越えており、 最終的な測定誤差は300%を越えてしまいそうである。 正解が誤差の範囲に含まれていると言っても、 その範囲が広過ぎるならば、測定は当てにならないことになってしまう。

図1. 俣野界面の報告値	図2. 微分の報告値	図3. 積分の報告値

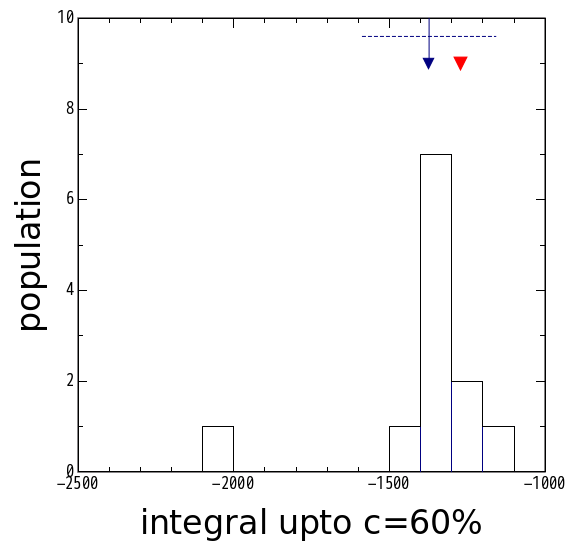
こんな時に備えて、積分や微分を計算する元になるデータも 報告してもらってある。 こちらの元データを用いて計算した微分と積分の値の分布を 図4及び図5に示す。 どちらも平均値と厳密解の差は1割前後であり、 データの散らばり(標準偏差)も厳密解の20%以内にある。 先程の大きな標準偏差は、 測定値から答を導く手順の錯誤のためであったと考えられる。

図4. 元データから計算し直した積分	図5. 元データから計算し直した微分

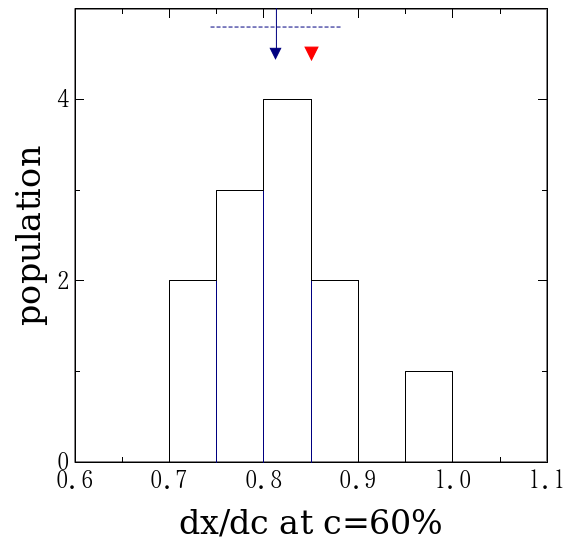
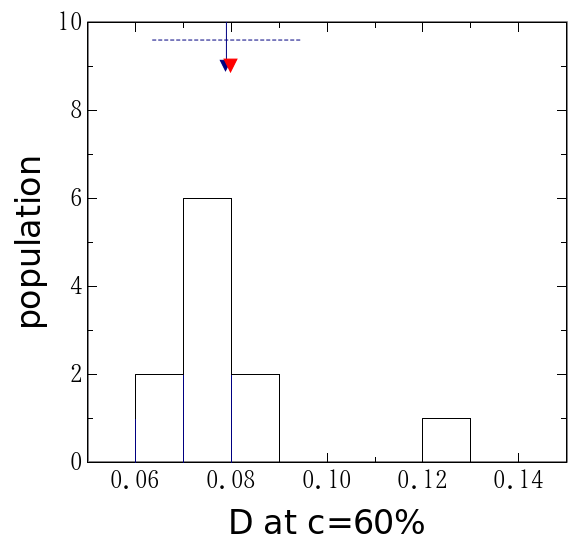
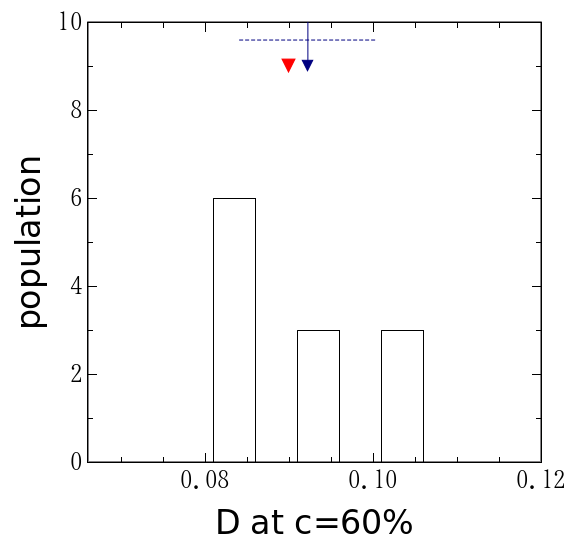
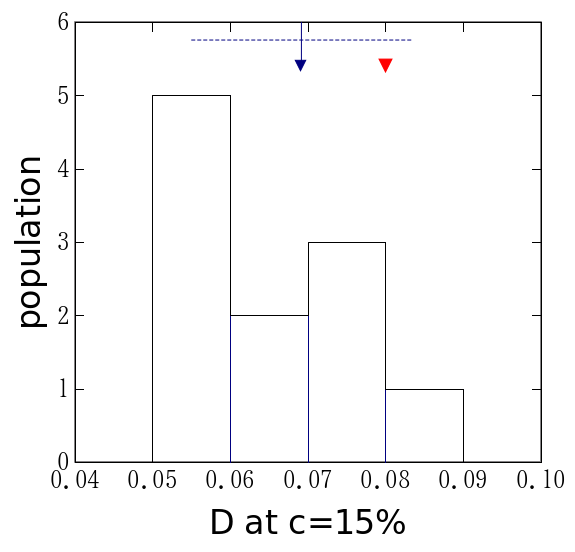
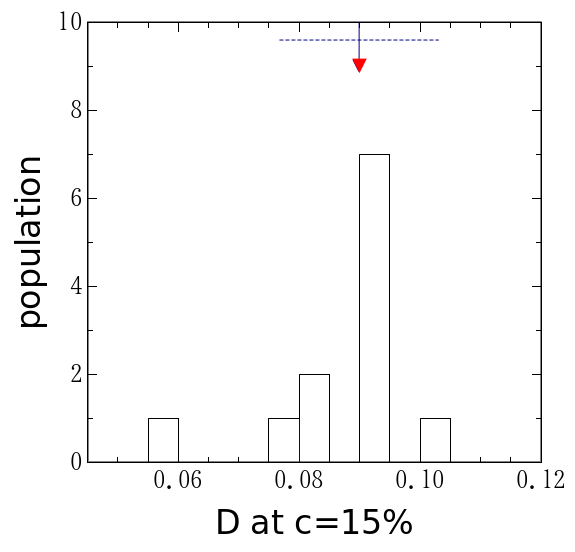
失敗をあげつらうためにこの実験をした訳ではないので、 これ以上続けるのは止めよう。 最終的に求めたい拡散係数の値の分布を図6に示した。 偶然測定値の平均が厳密解の非常に近くにあるものも存在するが、 まあ、偶然であろう。それ自体に重大な意味はない。 厳密値は測定の度に変えてあるが、何れの回にも概ね0.1位になるようにした。 それに対して標準偏差は各回とも0.01から0.02位であろうか。 平均値の1/10よりは少し大きなばらつきになっているが、 数倍といったずれは生じない。 今年度もテキストに書かれている「誤差は10∼20%」という目安は 機能してくれるものと考えられる。

60%での 拡散係数
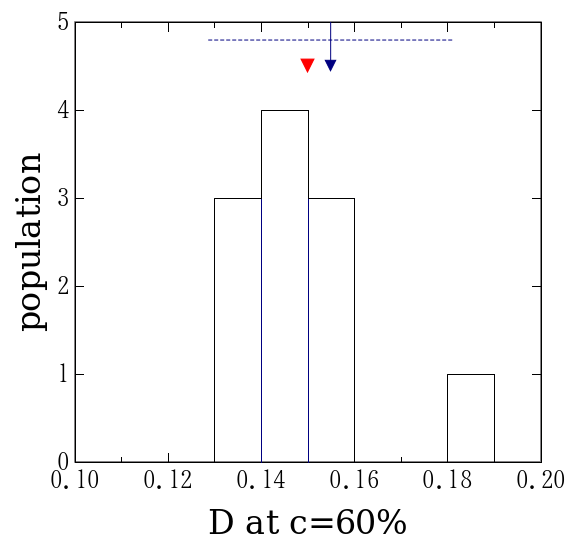15%での 拡散係数

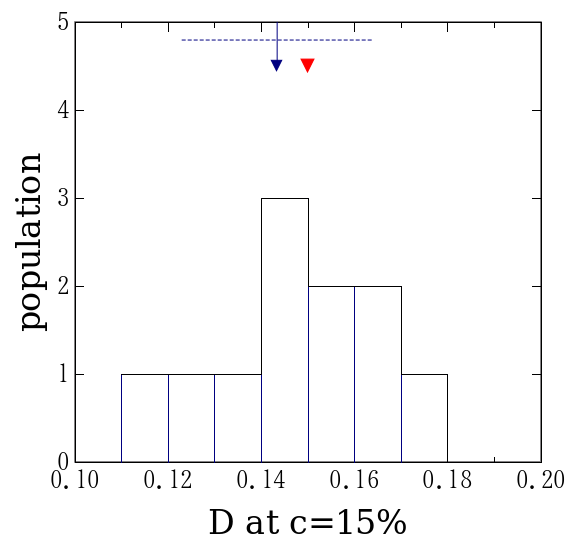図6. 拡散係数の値の分布